投影公式的推导

# 前言

今天偶尔看见有人说：点乘除了用于判断向量之间的相似度之外，还可用于投影的计算。

于是稍微看了下，貌似还真是！
通过推导投影公式，若其投影得边向量为归一化向量 (在游戏中直接 Normalize 就好了)，那可不就是么？

然后又推导了一下投影的公式，发现竟然可以算的上是 “异常” 简单了！

# 原理

首先，来看一张简单的图片吧：

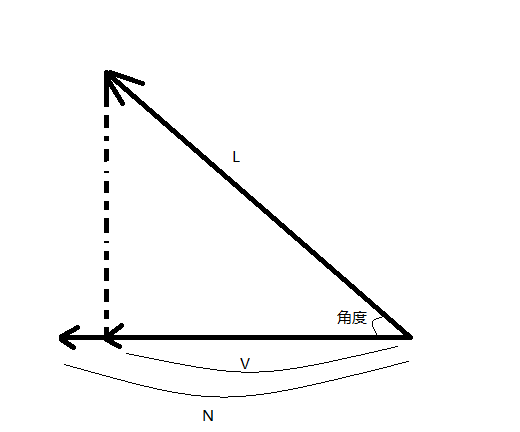
唔... 随便用 Windows 的画图工具画的，看看就好，差不多就是这样了。

其中：
N 即为底边的归一化向量，已知；
L 为斜边，已知；
V 为 L 在 N 上的投影向量 —— 我们需要求出的也就是这个了。

那么，第一个很重要重要的一点是：既然 N 已知并且为归一化向量，那么 V 的模，也就是底边的长度，乘以 N，是否就是 V 的向量了呢？
所以，只要能够计算出底边的长度，将底边长度乘以 N 向量，那么就可以得出 L 在 N 上的投影 V 了。

—— 基本原理就是这样。
接着，按照正常的三角形公式，把上边这个三角形的底边 V 的长度算出来差不多就结束了。

OK，然后，有一个大家都明白的公式：

$$Cos\theta={邻边 \over 斜边}$$

在这儿的表现就是：

$$Cos\theta={|V| \over |L|}$$

然后，转化一下下，得出：

$$|V|=Cos\theta \times |L|$$

此外，还有一个公式：点乘可以可以被分解成 $a \cdot b=|a||b|Cos\theta$

所以我们可以把它代入上述公式，可得：

$$|V|={Cos\theta \times |L| \times |N| \over |N|}$$

简单来说，就是直接乘上了一个 $|N| \over |N|$

这样，根据上面点乘公式，最后得出如下公式：

$$|V|={L \cdot N \over |N|}$$

因为上文我们已经说过了，是单位向量，那么 | N | 的值当然就是 1 了 (就算不是，到了这儿，也没多大差别了)，既然如此，就可以化简如下：

$$|V|={L \cdot N}$$

哦.... 这样子就求出底边 V 的长度来了！
然后，按照先前提到的，长度乘以单位向量 N，就得出最终公式：

\begin{align} V&=|V| \times N \\ &={(L \cdot N)} \times N \end{align}

Over。
就是这样。

在我的游戏生涯中，其实也就曾经写 V&F Shader 的时候，在计算高光反射向量的时候用到过（[$2N \times (L \cdot N)-L=R(反射向量)$] 当然如果是直接用 CG 语言内置函数 reflect... 的话... 那就算这儿也用不上了）。

原理就是这样简单。